How to break a contract
Heyo,
Jules here, from Cyfrin.
More than $1,000,000,000 has been stolen on-chain in 2023. This is not okay.
It’s why we’re open sourcing the ultimate security and auditing course at Cyfrin Updraft ⚡️. Start learning smart contract security for free today!
The course goes through fuzzing, manual review techniques, static analysis, how to build an audit report, how MEV works, how to leverage flashbots, and so much more.
One of the topics that doesn’t come up in this first section though is formal verification. For that one, we’ll have to wait for Part 2, but here’s a sneak peak! 😉
🧪 What is formal verification (FV) testing?
= The act of proving or disproving a given property of a system using a mathematical model.
Formal verification tries to break properties using mathematical proofs.
There are many different ways to do formal verification such as:
Symbolic execution (most popular in web3)
Abstract interpretation
Model Checking
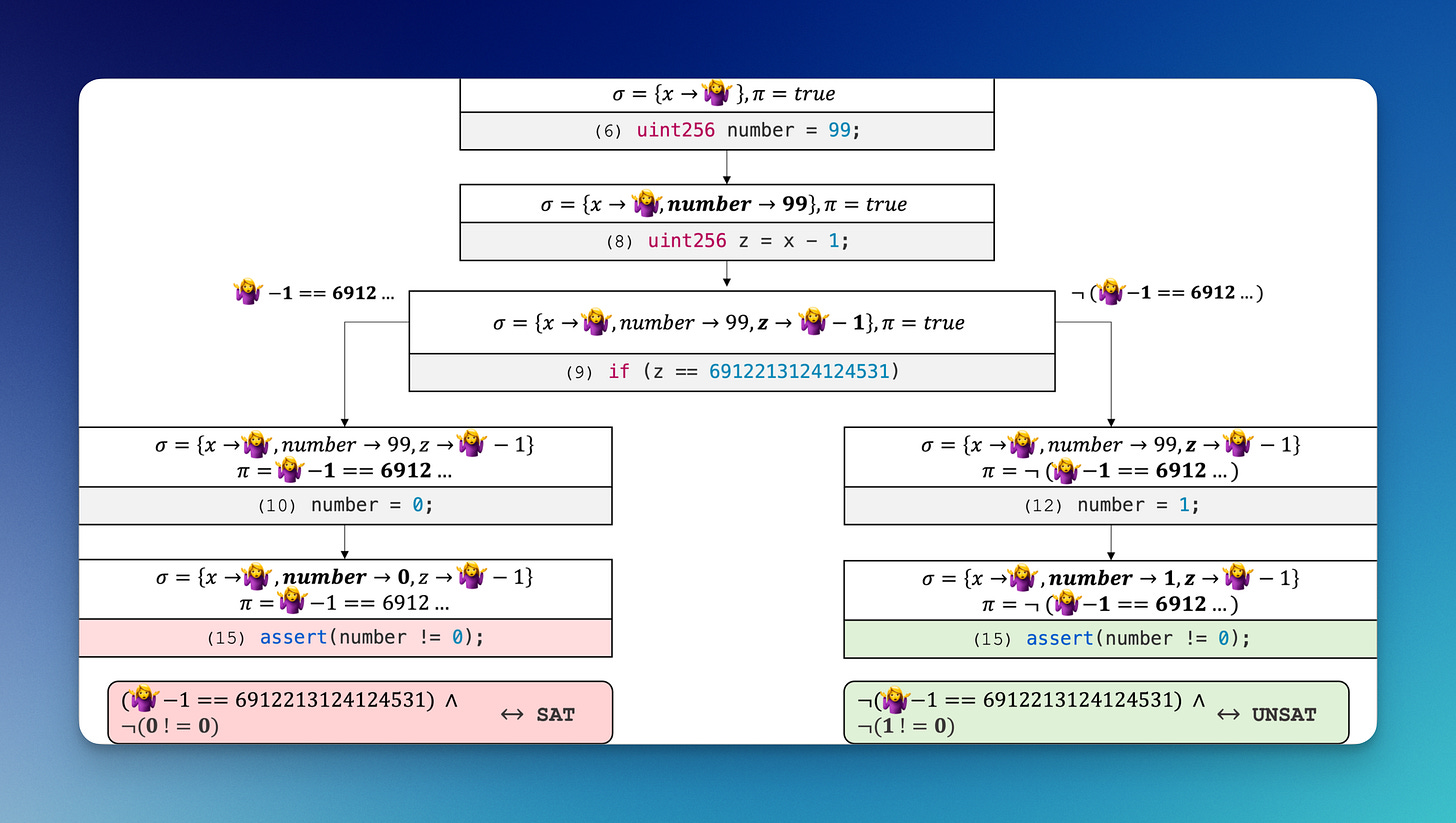
👩🏻💻 How to use symbolic execution for FV?
= Symbolic execution explores the different paths in a program, creating a mathematical representation for each path.
Symbolic execution makes your code math: it explores the different paths the program can take and represents them as mathematical expressions to try to prove something.
Here’s how to use it in 3 steps:
Define the invariant property and explore all paths
The invariant is the property you want to prove should be a certain way.
In this example - we have 2 paths, each with their own invariant:
Path 1: We return (a + 1)
Path 2: a + 1 overflows, so we must revert
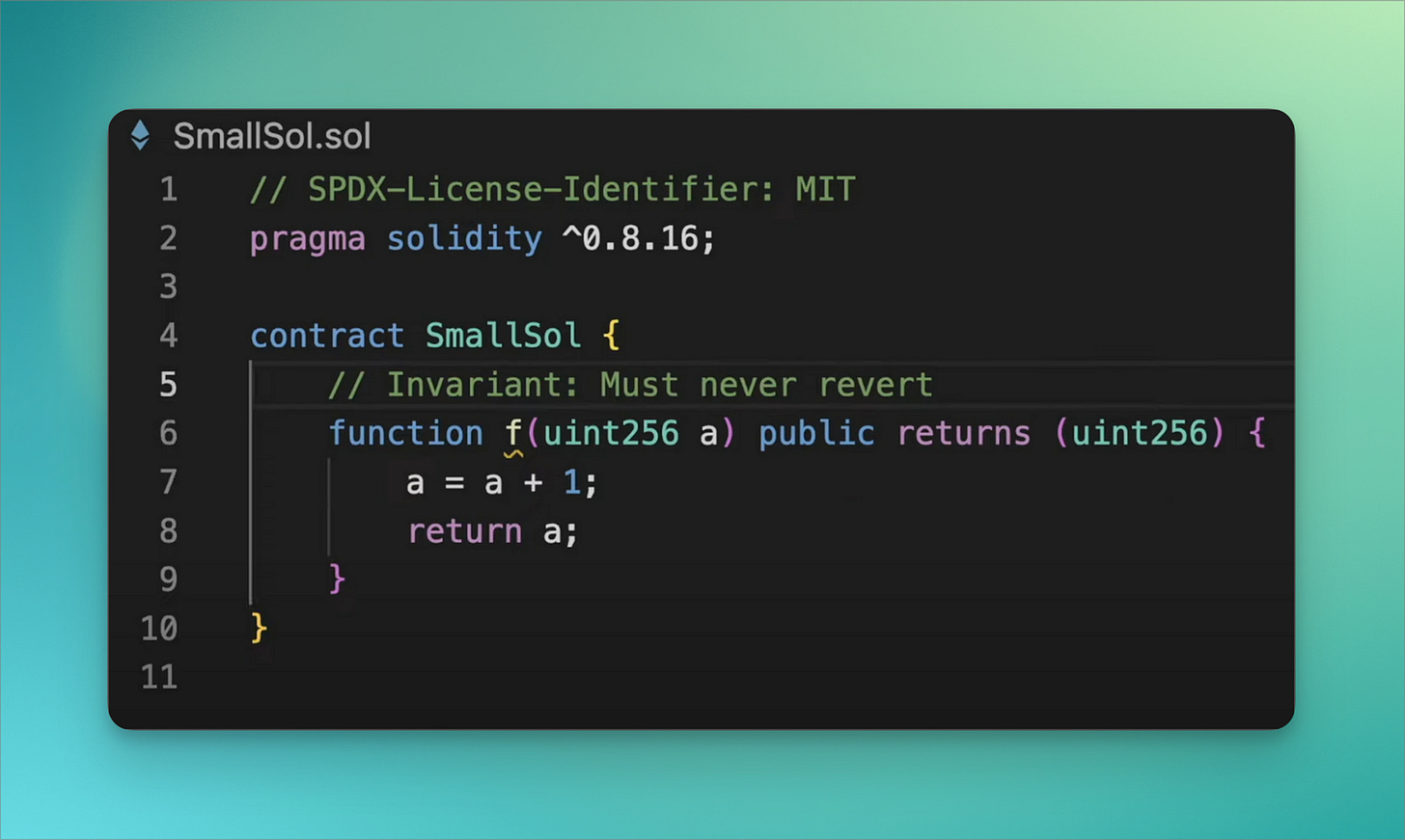
Convert paths to mathematical expressions
Some of the most common ways to converting paths to expressions is to turn them into booleans.
For the examples above, we may define our expressions something like:
Path 1: a < type(uint256).max
Path 2:
a == type(uint256).max
a + 1 < a
Run the mathematical expressions through a solver
Once we have the expressions, we run them through a solver, normally using a symbolic execution tool like Manticore, HEVM, and even the Solidity SMT checker.
A solver is used to determine if the path constraints can be satisfied and with which values.
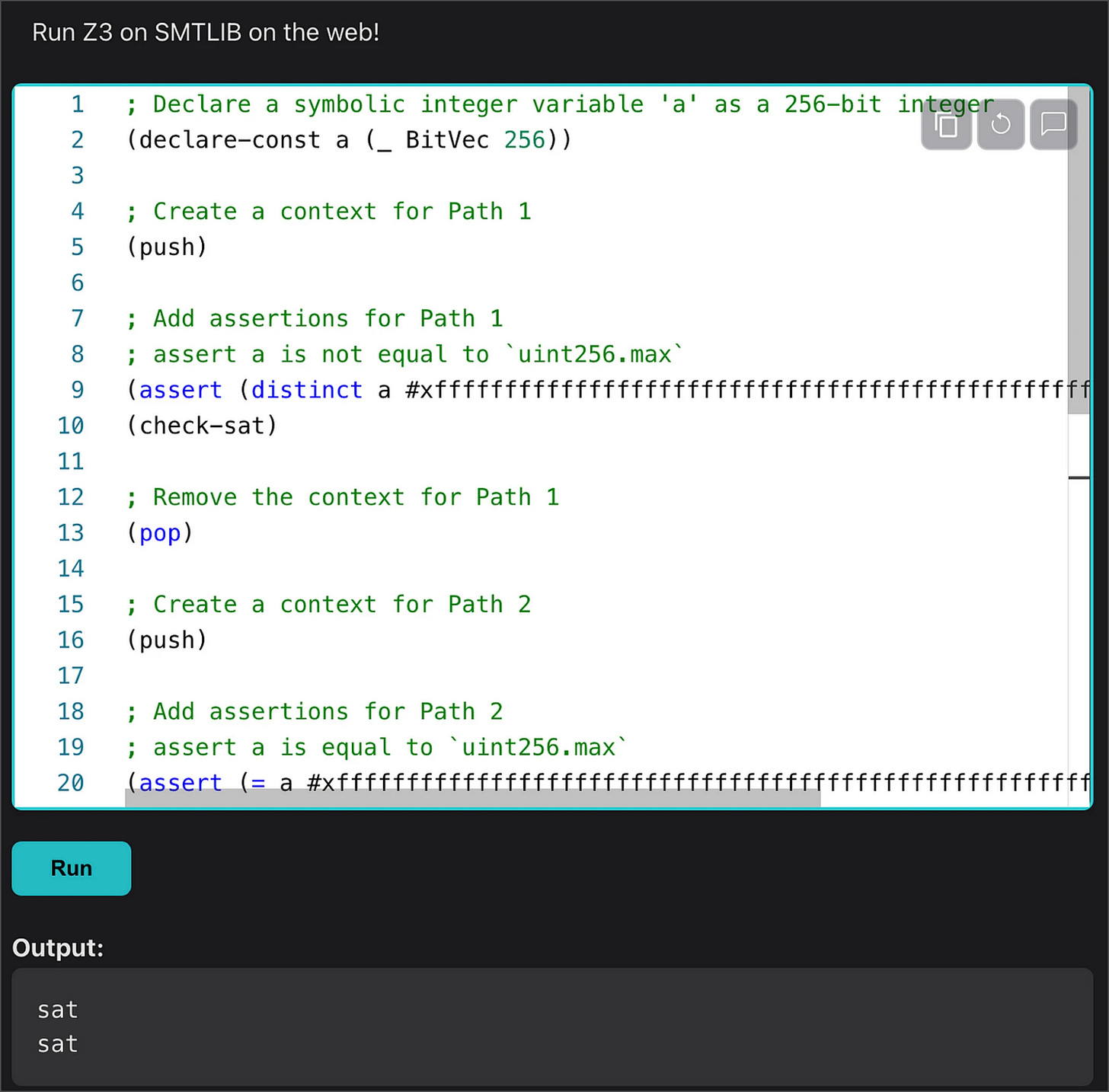
This is an example testing our invariantes using Z3 as our symbolic execution tool and solver.
The sat output means Z3 was able to find an input that makes the set of booleans for each path true — and since path 2 reverts, and our invariant is that it should never revert, we proved our invariant breaks!
💡 Some considerations
Formal verification takes a significant effort to set up right and it can be hard to maintain throughout time.
There’s also the path explosion problem for symbolic execution tools, which occurs when your program has too many paths for a computer to explore in a reasonable amount of time and the solver is never able to finish.
It depends on the invariants you define, so if you forget a property, your code is not bug-free.
— Check out the full article here: https://www.cyfrin.io/blog/formal-verification-symbolic-execution
Always feel free to reach out if there’s anything we can support or collaborate on.
Sending lots of cyber love,
Jules 🤸🏻



